[스터디/2019] Survey of Activation Functions
A. Activation Function이 가져야 할 바람직한 속성
Nonlinear
- activation function이 비선형(nonlinear)인 경우, 2개의 layer를 가진 신경망은 universal function approximator가 된다는 것이 증명됨(https://pdfs.semanticscholar.org/05ce/b32839c26c8d2cb38d5529cf7720a68c3fab.pdf).
- identity function은 선형이기 때문에 이러한 속성을 만족하지 못함. 여러 개의 layer들이 identity function을 사용하는 경우, 전체 network는 하나의 layer를 가진 model과 동일하게 됨.
- 참고: universal approximation theorem
- 한 개의 hidden layer를 가진 feed-forward network를 이용해 어떠한 함수든지 근사화시킬 수 있다는 이론임.
- 하지만, 해당 hidden layer 내 unit들의 크기는 감당할 수 없을 만큼 클 수도 있으며, 정확히 배우지 못하고 일반화를 하지 못할 수도 있음.
- 보다 깊은 모델을 사용하면 unit의 수를 줄이고 오차를 줄일 수 있음.
Range
- activation function의 범위(range)가 유한한 경우, 패턴 표현은 제한된 weight들에만 큰 영향을 주기 때문에 gradient 기반 훈련 기법들은 더 안정적인 경향이 있음.
- 반대로 범위가 무한한 경우, 패턴 표현은 대부분의 weight들에게 큰 영향을 주기 때문에 훈련이 일반적으로 보다 효율적이게 됨. 이 경우에는 보통 learning rates가 작아야 함.
Continuously differentiable
- 연속적인 미분 가능(continuously differentiable)은 gradient 기반 최적화 기법들을 가능하게 하는 바람직한 속성임.
- ReLU: 입력이 0 이하인 경우에는 gradient가 0이 되며, 입력이 0 초과인 경우에는 gradient가 1로 일정함. 이로 인해 gradient 기반 최적화 시 일부 문제가 있지만, 여전히 미분은 가능함.
- Binary Step: 입력이 0인 경우 미분이 불가능하며, 다른 입력들에 대해서는 gradient가 0이 됨. 따라서, gradient 기반 방법들로는 최적화를 할 수 없음(https://books.google.co.kr/books?id=0tFmf_UKl7oC&redir_esc=y).
Monotonic
- activation function이 단조(monotonic)일 경우 single-layer model와 연관된 error surface는 convex를 보장하게 됨(https://www.researchgate.net/publication/220311589_Global_stability_analysis_of_a_general_class_of_discontinuous_neural_networks_with_linear_growth_activation_functions).
- 참고
- 함수의 입력이 증가(또는 감소)함에 따라 결과가 함께 증가(또는 감소)하는 경우 “단조(monotonic) 증가(또는 감소)”한다고 해석하며 이를 monotonic하다고 표현함. 어떤 입력이 커질수록(또는 감소할수록) 어떤 경향을 보인다고 해석이 가능함.
Smooth functions with a monotonic derivative
- gradient가 단조인(monotonic derivative) 매끄러운 함수(smooth function)일 때 경우에 따라 일반화(generalization)가 더 잘된다고 알려져 있음.
- 참고
- monotonic derivative: 특정 함수를 나타내는 그래프의 gradient가 계속 증가(또는 감소)하는 경우에만 monotonic derivative하다고 표현함. 어떤 입력의 gradient가 증가(또는 감소)하는 구간이 있기 때문에 경향을 알 수 없다고 해석함.
- smooth functions: 해석학에서, smooth function은 무한 번 미분이 가능한 함수를 말함. 미분 가능은 연속적(continuous)이어야 하고 그 점에서 미분 계수가 같으므로 매끄럽게(smooth) 연결됨을 알 수 있음.
Approximates identity near the origin
- activation function이 origin 근처에서 항등 사상(identity mapping)을 근사화하는 속성이 있으면, neural network은 weights가 작은 임의(small random)의 값들로 초기화 될 때 효율적으로 학습됨. 반대로 origin 근처에서 항등 사상을 근사화 하지 못하면, weights를 초기화 할 때 특별한 주의가 필요하게 됨(https://arxiv.org/abs/1412.6558).
- 추가 자료: https://stats.stackexchange.com/questions/288722/why-activation-functions-that-approximate-the-identity-near-origin-are-preferabl?rq=1
B. 다양한 종류의 Activation Function들에 대한 계산식
- 사각형: activation function의 group을 의미
- 점선: 원래 activation function과 변종 activation function의 구분을 의미

C. Activation Function의 종류
1. Sigmoid Function
* Features
- 몇몇 문헌들에서는 logistic function 또는 squashing function이라고도 불림(https://pdfs.semanticscholar.org/823b/c07f2a305aca73a0a8140937280a0265fda8.pdf).
- Hard Sigmoid Function, Sigmoid-Weighted Linear Units(SiLU), Derivative of Sigmoid-Weighted Linear Units(dSiLU) 등의 3가지의 변종이 존재함.
- feedforward neural networks에서 사용되는 non-linear activation function임.
- 실수 입력 값에 의해 정의된 미분 가능한 경계를 가지는 real function으로, 모든 곳에서 positive derivative하며, 약간의 degree of smoothness를 가짐(https://link.springer.com/chapter/10.1007/3-540-59497-3_175). 계산식은 다음과 같음.
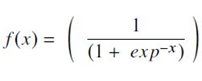
- deep Learning 아키텍처에서 보통 output layer에 사용되며, output에 대한 확률을 예측하는데 사용됨. 출력 값의 범위는 0~1 사이로 제한됨.
* Pros
- binary classification 문제, logistic regression 모델링, 기타 neural network 도메인 등에서 성공적으로 적용되었음.
- 이해 하기 쉽고 대부분의 shallow network에서 사용됨(http://www.cs.toronto.edu/~bonner/courses/2016s/csc321/readings/Connectionist%20learning%20of%20belief%20networks.pdf).
- small random 값들에 의해 neural network를 초기화시키는 경우를 피할 수 있음(http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf).
* Cons
- “hidden layers에서 input layers로 gradient를 backpropagation 시 sharp하고 damp한 gradient를 가짐, gradient saturation, 수렴이 느림, 출력의 중심이 0이 아님” 등의 이유로 gradient update 시 다른 방향으로 propagation됨.
- Sigmoid function의 위와 같은 단점을 극복하기 위해 Hyperbolic tangent function이 제안됨
1.1) Hard Sigmoid Function
* Features
- Sigmoid function의 hard한 변종임.
- Soft Sigmoid function과 비교 했을 때 계산비용이 적으며, deep learning 기반의 binary classification task에서 희망적인 결과를 보임(https://arxiv.org/pdf/1511.00363.pdf). 계산식은 다음과 같음
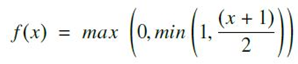
1.2) Sigmoid-Weighted Linear Units(SiLU)
* Features
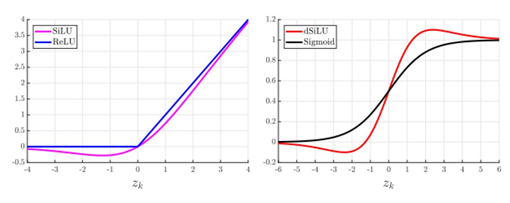
- reinforcement learning을 기반으로 하는 approximation function으로서, Sigmoid에 입력 값을 곱한 값으로 계산이 됨(https://arxiv.org/abs/1702.03118). 계산식은 다음과 같음. s는 input vector이며, z_k 는 hidden unit k에 대한 input을 나타냄.
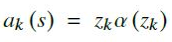
- deep neural network의 hidden layers에서만 사용이 되며, reinforcement learning 기반 시스템에서만 사용됨.
1.3) Derivative of Sigmoid-Weighted Linear Units(dSiLU)
* Features
- SiLU의 gradient로서, gradient-descent learning 시 neural network의 weight parameters를 update하는데 사용됨. 계산식은 다음과 같음.
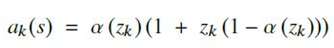
- dSiLU의 response는 다음 그림과 같이 overshooting Sigmoid function처럼 보이며, standard Sigmoid function보다 상당히 우수한 결과를 보임(https://arxiv.org/abs/1702.03118).
2. Hyperbolic Tangent Function(Tanh)
* Features
- Tanh function으로도 알려져 있으며, smoother(https://www.nature.com/articles/nature14539) zero-centered function으로서, 출력 값의 범위는 -1~1 사이로 제한됨.
- 계산식은 다음과 같이 주어지며, 변종으로는 Hard Hyperbolic Function이 있음.
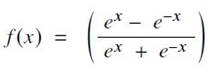
- 자연어 처리(https://arxiv.org/pdf/1612.08083.pdf) 및 음성 인식(https://ai.stanford.edu/~amaas/papers/relu_hybrid_icml2013_final.pdf) task를 위한 recurrent neural networks에서 대부분 사용됨.
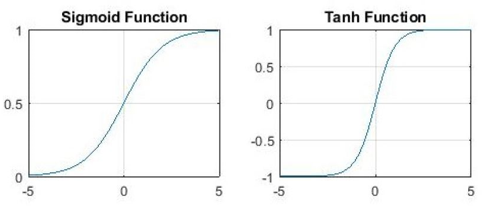
- Sigmoid 및 Tanh activation function의 차이는 다음 그림과 같음.
* Pros
- multi-layer neural network에 대한 훈련 성능이 더 좋기 때문에 Sigmoid function보다 선호되는 function임(http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.740.9413&rep=rep1&type=pdf, https://www.sciencedirect.com/science/article/abs/pii/0004370292900656?via%3Dihub).
- 출력의 중심이 0이기 때문에 back-propagation 처리를 도울 수 있음.
* Cons
- Sigmoid function과 유사하게 vanishing gradient 문제를 해결하지 못함.
- 입력 값이 0일 때만 gradient가 1이 되며, 이는 계산 중에 dead neuron을 일부 생성하게 함.
- dead neuron은 gradient가 0이 되어 activation weight가 사용되지 않는 상태를 말하며, 이러한 한계로 인해 Rectified Linear Unit(ReLU) activation function이 탄생됨.
2.1) Hard Hyperbolic Function
* Features
- Hardtanh function으로도 알려져 있으며, Tanh function의 계산적인 효율성을 고려한 version임. 출력의 범위는 -1~1 사이로 제한되어 있으며, 계산식은 다음과 같음.
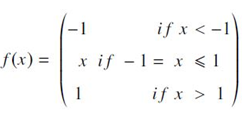
- 자연어 처리에서 성공적으로 적용되었으며, 속도 및 정확도가 개선되었음(http://www.jmlr.org/papers/volume12/collobert11a/collobert11a.pdf).
3. Softmax Function
* Features
- 실수 값을 가지는 vector로부터 확률 분포를 계산하는데 사용되며, 0~1 사이의 출력 값을 가짐(http://www.deeplearningbook.org/). 출력 값들의 총합은 1이 되며, 계산식은 다음과 같음.
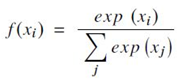
- 각 class에 대한 확률을 반환하는 multi-class model에 사용되며, target class는 가장 높은 확률을 갖게 됨. deep learning 아키텍처의 output layer에서 주로 사용됨(https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf, https://arxiv.org/abs/1511.00561, https://arxiv.org/abs/1312.4400).
- Sigmoid와 Softmax의 가장 큰 차이는 Sigmoid는 binary classification에서 사용되는 반면에 Softmax는 multivariate classification task에서 사용된다는 점임.
4. Softplus Function
* Features
- ReLU function의 smooth version으로서, smoothing 및 nonzero gradient의 속성을 가지고 있음.
- (https://papers.nips.cc/paper/1920-incorporating-second-order-functional-knowledge-for-better-option-pricing.pdf)에서 제안되었으며, Sigmoid function의 원시적인(primitive) 형태임. relationship은 다음과 같음.
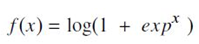
5. Softsign
* Features
- (https://pdfs.semanticscholar.org/823b/c07f2a305aca73a0a8140937280a0265fda8.pdf)에서 도입된 nonlinear activation function이며, 이차 다항식(quadratic polynomial) function으로서 계산식은 다음과 같음.
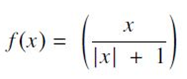
- Softsign과 Tanh function의 주된 차이는 Softsign은 polynomial form로 수렴하지만, Tanh function은 exponentially하게 수렴한다는 것임.
- regression 계산 문제들(https://www.aclweb.org/anthology/S15-1002/)에서 대부분 사용되며, deep learning 기반 음성 시스템(https://arxiv.org/abs/1710.07654)에서도 사용이 되었고 희망적인 결과를 보여줌.
6. Rectified Linear Unit(ReLU) Function
* Features
- 최근까지 state-of-the-art의 결과를 보이는 deep learning 어플리케이션에서 가장 많이 사용되는 activation function으로서 (https://www.cs.toronto.edu/~fritz/absps/reluICML.pdf)에서 제안됨.
- Leaky ReLU(LReLU), Parametric Rectified Linear Units(PReLU), Randomized Leaky ReLU(RReLU), S-shaped ReLU(SReLU) 등의 4가지 변종이 존재함.
- 다른 종류의 activation function들과 함께 deep neural network의 hidden unit 내에서 사용되거나 객체 분류(https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf, https://arxiv.org/abs/1502.01852) 및 음성 인식 어플리케이션(https://ai.stanford.edu/~amaas/papers/relu_hybrid_icml2013_final.pdf)에서 network의 output layer에서 사용이 됨.
- ReLU 및 변종들은 단순함과 신뢰성으로 인해 다음과 같은 다양한 deep learning 아키텍처에서 사용되었음.
- restricted Boltzmann machines(https://www.cs.toronto.edu/~fritz/absps/reluICML.pdf)
- convolutional neural network(https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf, https://arxiv.org/abs/1409.4842, https://arxiv.org/abs/1502.01852, https://arxiv.org/abs/1311.2901, https://www.ncbi.nlm.nih.gov/pubmed/29144388)
* Pros
- 빠른 학습이 가능하며(https://www.nature.com/articles/nature14539), 가장 성공적으로 널리 사용되는 activation function임이 증명됨(https://arxiv.org/abs/1710.05941).
- Sigmoid나 Tanh activation function에 비해서 보다 우수한 성능 및 일반화(generalization)를 보임(https://ieeexplore.ieee.org/document/6638312, https://wiki.eecs.yorku.ca/user/hj/_media/publication:p6899-zhang.pdf).
- 거의 linear function에 가깝기 때문에, gradient-descent 기법을 이용하여 최적화를 쉽게 할 수 있는 linear model의 속성을 보존할 수 있음(http://www.deeplearningbook.org/). 계산식은 다음과 같음.
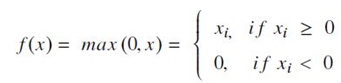
- 0보다 작은 입력 값을 강제로 0으로 만들어 출력함으로써, 초기의 activation function들이 가졌던 vanishing gradient 문제를 제거함.
- exponentials 및 division을 계산하지 않기 때문에 빠른 계산을 보장하므로 전체적인 계산 속도를 향상시킬 수 있음(https://ieeexplore.ieee.org/document/6638312).
- 0에서 최대 사이의 범위를 가지는 값들을 뭉개버림(squishes)으로써 hidden units에 희소성(sparsity)을 도입시킬 수 있음.
* Cons
- ReLU의 overfitting 영향을 줄이기 위해 dropout 기법이 적용되고 rectified networks가 deep neural network의 성능을 향상시키긴 했지만(http://proceedings.mlr.press/v15/glorot11a/glorot11a.pdf), Sigmoid function에 비해 쉽게 overfitting 되는 한계가 있음.
- 일부 gradient가 죽어버리기 때문에 훈련이 지속적으로 되지 않는 분명한 한계가 있음. 이로 인해 일부 neuron들이 dead 상태가 되어 향 후 data points에서 weight update가 활성화 되지 않고, dead neuron이 zero activation을 제공하기 때문에 학습에 방해를 야기함(http://www.deeplearningbook.org/).
- dead neuron 문제를 해결하기 위해, leaky ReLU가 제안됨.
6.1) Leaky ReLU(LReLU)
* Features
- 전체 propagation 과정 동안에 weight update를 유지 및 지속하기 위해 ReLU에 작은 negative slope를 도입함(https://ai.stanford.edu/~amaas/papers/relu_hybrid_icml2013_final.pdf).
- alpha parameter를 ReLU의 dead neuron 문제에 대한 solution으로 도입함으로써, 훈련 동안에 gradient가 0이 되지 않게 됨.
- negative gradient에 매우 작은 상수 α (=0.01)를 이용하여 gradient를 계산하게 되며, 계산식은 다음과 같음.
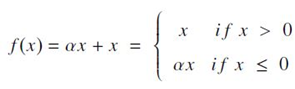
- 훈련 동안에 0이 아닌 gradient를 갖는다는 것을 제외하고는 standard ReLU와 동일한 결과를 가짐. 따라서 standard ReLU와 Tanh function과 비교했을 때 희소성(sparsity) 및 분산(dispersion)을 가진다는 점을 빼면 상당한 결과 개선은 없음(https://ai.stanford.edu/~amaas/papers/relu_hybrid_icml2013_final.pdf). 자동 음성 인식 dataset에 대해서 실험되었음.
6.2) Parametric Rectified Linear Units(PReLU)
* Features
- function의 negative part는 적응적으로 학습되며, positive part는 linear한 속성을 갖고 있음(https://arxiv.org/abs/1502.01852). 계산식은 다음과 같음.
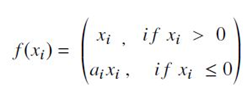
- a_i 는 negative slope를 control하는 parameter이며, back-propagation을 이용하여 훈련하는 동안 학습이 가능함. term a_i =0인 경우에는 PReLU는 ReLU와 같게 됨.
- PReLU는 large scale image recognition에 있어서 ReLU보다 성능이 우수하며, PReLU를 적용한 visual recognition challenge에서 사람 수준의 성능을 처음으로 넘어서게 됨(https://arxiv.org/abs/1502.01852).
6.3) Randomized Leaky ReLU(RReLU)
* Features
- leaky ReLU의 동적인 변종(dynamic variant)으로서, uniform distribution U(l, u) 로부터 샘플링된 random number가 network를 훈련시키는데 사용됨. 계산식은 다음과 같음.
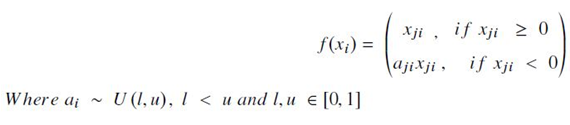
- test 단계에서는 학습된 parameter에 사용된 dropout을 deterministic value로 사용하지 않고, 훈련에서와 같이 모든 a_ji에 대한 평균화 기법(averaging technique)을 사용하며, 이는 a_ji= (l+u)/2로 얻을 수 있음. 따라서 실제 test output은 다음 relationship으로 얻을 수 있음.
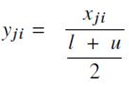
- RReLU는 standard classification datasets에 대해 실험 및 ReLU의 여러 변종들과 비교되었으며, classification tasks에서는 LReLU, RReLU, PReLU 등이 ReLU보다 우수하다는 것이 검증됨(https://arxiv.org/abs/1505.00853).
6.4) S-shaped ReLU(SReLU)
* Features
- 신경과학(neural sciences) 및 정신물리학(psychophysics) 법칙(laws)에서 영감을 얻은 activation function으로서, convex 및 non-convex function을 모두 학습시키기 위해 사용됨.
- backpropagation을 이용하여 deep neural network를 훈련하는 동안 학습되는 4개의 학습 가능한(learnable) parameters들로 구성된 3-piece의 wise linear function들로 이루어져 있음(https://arxiv.org/pdf/1512.07030.pdf). 다음의 mapping relationship을 이용하여 얻을 수 있음.
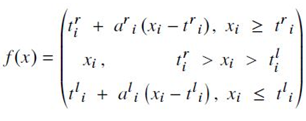
- t^l_i, t^r_i, a^l_i 은 network에서 학습 가능한(learnable) parameter들을 의미하며, i 는 SReLU가 channel마다 다를 수 있다는 것을 의미함.
- a^r_i은 설정된 threshold를 초과하는 입력을 갖는 우측 선의 slope를 나타내며, t^r_i,, t^l_i 은 각각 positive 및 negative 방향의 threshold를 나타냄.
- GoogLeNet을 이용한 Network In Network 아키텍처에 적용되었으며, CIFAR-10, ImageNet, MNIST standard datasets 등과 같은 image recognition task에 대해 다른 activation functions들에 비해 개선된 결과를 보여줌(https://arxiv.org/pdf/1512.07030.pdf).
7. Exponential Linear Units(ELUs)
* Features
- deep neural network의 훈련 속도를 빠르게 하기 위해 사용됨.
- 변종으로는 Parametric Exponential Linear Units(PELU), Scaled Exponential Linear Units(SELU) 등이 있음.
* Pros
- positive values들에 대해 identity를 사용함으로써 vanishing gradient 문제를 경감시킬 수 있으며, 학습 특성(characteristics)을 개선시킬 수 있음.
- mean unit activation을 0에 가깝도록 push하여 계산상의 복잡성을 줄이고 학습 속도를 향상시킬 수 있는 negative values들을 가짐(https://arxiv.org/abs/1511.07289).
- 훈련 동안 mean activation을 0으로 push하여 bias shift를 감소시킬 수 있기 때문에, ReLU의 좋은 대안이 될 수 있음. 계산식은 다음과 같이 주어짐.
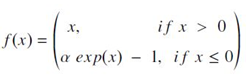
- α는 negative net input에 대해 saturation points를 control하는 hyperparameter로서 보통 1.0으로 설정함.
- negative 체제(regime)에서 분명한 saturation 고원(plateau)을 가지고 있기 때문에, 보다 강건한 표현(representations)을 학습할 수 있음. 특히 5개 layer 이상의 특정한 network 구조를 가진 ReLU 및 LReLU에 비해 좀 더 빠른 학습 속도와 좀 더 나은 일반화(generalization)를 제공함. 또한, ReLU의 변종들에 비해 state-of-the-art 결과를 보장함.
* Cons
- 출력의 중심이 0이 아닌 결정적인 한계가 있으며, 이러한 문제를 다루기 위해 parametric ELU가 제안됨.
7.1) Parametric Exponential Linear Units(PELU)
* Features
- (https://arxiv.org/pdf/1605.09332v1.pdf)에서 제안되었으며, ELU에서 나타난 출력의 중심이 0이 아닌 문제를 다루고 있음.
- vanishing gradient 맥락(context)에서 출력의 중심을 0으로 유지하면서, bias shift를 줄이는데 사용되는 gradient 기반 최적화 프레임워크를 제공함.
- ELU에 비해 2개의 추가적인 parameter를 가지고 있으며, 계산식은 다음과 같음.
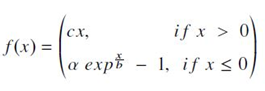
- α, b, c는 모두 0보다 크며, c가 positive quadrant에서 slope의 변화를 발생시키는 경우, b는 exponential decay의 scale을 control하고, α는 negative quadrant의 saturation을 제어함.
- α, b, c를 모두 1로 설정하면, original ELU activation function과 동일함.
* Pros
- CNN과 같이 적은 bias shifts와 vanishing gradients를 필요로 하는 어플리케이션에 적합한 선택이 될 수 있음.
7.2) Scaled Exponential Linear Units(SELU)
* Features
- (https://arxiv.org/pdf/1706.02515v5.pdf)에서 제안되었으며, self-normalising 특성을 유도하는 독특한 성질을 갖는 self-normalising neural network로서 도입되어짐.
- network를 훈련 중에 여러 layers들을 통해 propagation 시 zero mean과 unit variance를 향해 수렴하는 0에 가까운 mean과 unit variance를 가지고 있으므로, deep learning 어플리케이션에 적합하며, 강력한 regularisation을 통해 강건한 feature들을 효율적으로 학습할 수 있음. 계산식은 다음과 같이 주어짐.
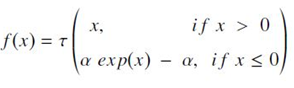
- 여기서 τ는 scale factor를 의미하며, parameter들에 대한 근사값은 α ≈ 1.6733, λ ≈ 1.0507 과 같음.
* Pros
- vanishing gradient 및 exploding gradient 문제에 영향을 받지 않음.
- ReLU, scaled ReLU, sigmoid, LReLU, tanh functions들로는 도출할 수 없는 self normalizing neural networks의 특성을 갖도록 mapping construction을 할 수 있게 해줌.
- classification tasks(https://arxiv.org/pdf/1706.02515v5.pdf) 및 심층 유전 돌연변이(deep genetic mutation) 계산(https://dl.acm.org/citation.cfm?doid=3205455.3205473) 등에 성공적으로 적용됨.
8. Maxout Function
* Features
- neural network의 weight와 data 간의 dot product를 적용하여 non-linearity이 만들어짐.
- (https://arxiv.org/pdf/1302.4389.pdf)에서 제안되었으며, network 계산 시 dying neuron 이나 saturation이 없는 ReLU와 leaky ReLU의 특성을 neuron이 상속할 수 있도록 ReLU 및 leaky ReLU를 일반화(generalization) 함. 계산식은 다음과 같음.
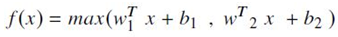
- phone recognition 어플리케이션(https://link.springer.com/article/10.1186/s13636-015-0068-3)에서 성공적으로 실험되었음.
* Cons
- 모든 neuron에서 사용되는 parameter를 두 배로 늘림으로써, network에서 계산할 parameter들의 수를 늘리게 되면 많은 계산 비용이 들게 됨.
9. Swish Function
* Features
- hybrid activation function을 만들기 위해 sigmoid activation function과 input function의 조합으로 제안된 최초의 compound activation function임.
- (https://arxiv.org/abs/1710.05941)에서 제안되었으며, function을 계산하기 위해 reinforcement learning 기반의 automatic search 기법을 사용함.
- smoothness, non-monotonic, 아래는 경계가 있으며(bounded below), 상한은 경계가 없는(unbounded in the upper limits) 성질을 가지고 있음. smoothness 속성은 swish function이 deep learning 아키텍처를 훈련 할 때 보다 나은 최적화(optimization) 및 일반화(generalization) 결과를 생성할 수 있도록 해줌. 계산식은 다음과 같음.
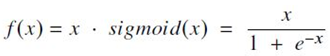
* Pros
- 훈련 동안에 우수한 information propagation을 제공하며, vanishing gradient 문제를 겪지 않기 때문에 단순함과 향상된 정확성을 가지게 됨. deep learning 기반 classification task에서 ReLU activation function 보다 우수한 결과를 보여줌.
10. ELiSH
* Features
- (https://arxiv.org/pdf/1808.00783.pdf)에서 제안된 가장 최신의 activation function으로서, Swish function과 공통된 특성들을 공유하고 있음.
- 변종으로는 HardELiSH가 있음.
- ELU와 Sigmoid function으로 구성이 되며, 계산식은 다음과 같음.
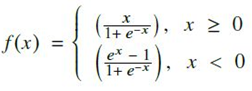
* Pros
- limit에 의해 정의된 negative 및 positive part가 변화하는 속성을 가지고 있음. Sigmoid part는 정보 흐름을 개선시키는 반면, linear part는 vanishing gradient 문제를 제거시킴.
- 서로 다른 deep convolutional 아키텍처를 이용하여 ImageNet 데이터셋에 성공적으로 적용되었음(https://arxiv.org/pdf/1808.00783.pdf)
10.1) HardELiSH
- (https://arxiv.org/pdf/1808.00783.pdf)에서 제안됨
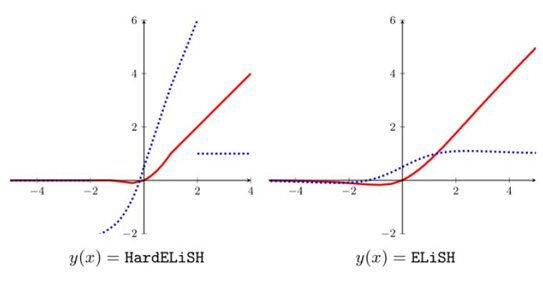
- ELiSH activation function의 hard한 변종으로서, negative part에서는 Hard Sigmoid와 ELU의 곱셈을 취하며, positive part에서는 Linear와 Hard Sigmoid의 곱셈을 취함. 계산식은 다음과 같음.
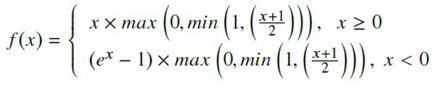
- ImageNet classification 데이터셋에 대해서 실험이 되었음.
- ELiSH와 HardELiSH function의 response 차이는 다음과 같음.
D. Backbone 아키텍처들에서 사용된 activation function의 종류 및 위치
|
Backbone |
Hidden layers |
Output layer |
Papers |
|
AlexNet |
ReLU |
Softmax |
2012 |
|
NiN |
No activation |
Softmax |
2013 |
|
ZFNet |
ReLU |
Softmax |
2013 |
|
VGGNet |
ReLU |
Softmax |
2015 |
|
SegNet |
ReLU |
Softmax |
2015 |
|
GoogleNet |
ReLU |
Softmax |
2015 |
|
SqueezeNet |
ReLU |
Softmax |
2016 |
|
ResNet |
ReLU |
Softmax |
2016 |
|
ResNeXt |
ReLU |
Softmax |
2017 |
|
MobileNets |
ReLU |
Softmax |
2017 |
|
SeNet |
ReLU |
Sigmoid |
2017 |
- 실용적인 deep learning 어플리케이션에서 사용된 activation functions들은 ReLU와 Softmax function들이 대다수를 이루고 있음.
- 대부분의 backbone들에서 ReLU는 hidden layers들에서 사용되고 있으며, Softmax function은 output layer에서 사용되고 있음. 하지만, SeNet과 같은 최신 backbone은 output layer에서 prediction을 달성하기 위해 Sigmoid function을 사용하기도 함.
- 가장 최근에 연구된 activation function들은 linear unit이며, rectified 및 exponential 변종을 갖는 총 8개의 변종 activation function들이 있음. 이들의 종류는 ReLU, LReLU, PReLU, RReLU, SReLU, ELU, PELU, SELU 등과 같음.
- ELU 및 변종들은 ReLU 및 변종들에 비해 빠른 학습 속도를 가지고 있으며, 이는 (https://arxiv.org/pdf/1804.02763.pdf)에서 MINST 데이터셋을 이용하여 ELU 및 ReLU의 변종들에 대한 포괄적인 비교를 통해 검증이 됨.
- PELU와 PReLU는 2개의 다른 parametric activation functions들로서 exponential 및 linear unit을 이용하여 개발되었고 둘 다 학습 가능한(learnable) parameter들을 가지고 있음.
- deep learning 어플리케이션에서 가장 일관적인 activation functions인 ReLU보다 더 우수한 성능을 나타내는 다른 종류의 activation function들이 있다는 것은 분명한 사실임.
- (https://arxiv.org/pdf/1505.00853.pdf)에서는 ReLU의 다른 변종인 LRELU, PReLU, RReLU이 ReLU보다 성능이 우수하다는 것을 검증했지만, 이러한 결과를 뒷받침할만한 이론적인 정당성은 결여되어 있음.
- parametric activation functions들은 데이터셋으로부터 학습 가능한(learnable) parameter로 activation function들을 사용했던 emerging한 어플리케이션에서 개발되어 왔기 때문에, SReLU, PELU, PReLU 등에서 관찰된 바와 같이 가장 최근에 개발된 새로운 functions에 대한 유망한 접근 방식이라 할 수 있음.
- deep leaning 어플리케이션에서 activation function 사용과 관련하여 가장 주목할만한 점은 새롭게 제안된 activation function들이 ReLU와 같은 이전의 activation functions들을 능가하는 것처럼 보이지만, 여전히 최신 아키텍처들도 ReLU function에 의존한다는 것임. 이는 SeNet에서 hidden layers들에서는 ReLU를 사용하고 output layer에서는 Sigmoid를 사용한 것을 보면 알 수 있음(https://www.microsoft.com/en-us/research/wp-content/uploads/2017/07/Look-Closer-to-See-Better-Recurrent-Attention-Convolutional-Neural-Network-for-Fine-grained-Image-Recognition.pdf).
- 현재의 관행은 새롭게 개발된 최신의 activation functions들을 사용하기 보다는 실험을 통해 입증된 activation functions들을 의존적으로 사용하기 때문에 새롭게 개발된 activation functions들은 실제로 거의 사용되고 있지 않음.